There is a lot of financial or investment tools in the market to help you achieve your financial goal with a peace of mind. However, some unscrupulous financial advisors or agents may just be more concerned about their sales target or bottom line instead of yours might feint you if you totally have no idea on the concept or calculation of compound interest (time value or money).
For example, investment advisor who just wanna close the sale may mislead you about the actual return of a saving plan, such as plan where you save $10,000 in one lump sum, and after 20 years you can get back a total return of $20,000. On paper, 20k return – 10k capital will equal to 10k profit. 100% profit divided by 10 years period equal to 10% interest rate annually. Is it true? No, this is definitely a misleading calculation for compounding interest. To stay away from the financial trap, you’re strongly advised to learn more about the how compound interest works. For your knowledge, it’s possible to use some Microsoft Office Excel functions to easily, accurately calculate the exact rate related to time value of money.
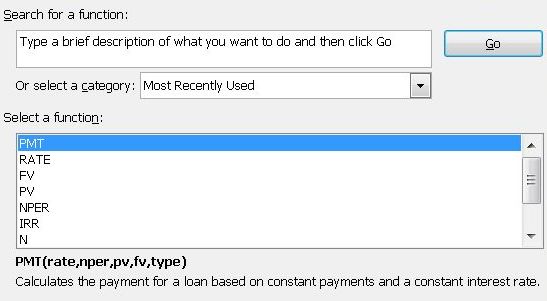
Firstly, you need to know more about some Microsoft Excel’s functions like:
- PV – Present value – formula: PV(rate,nper,pmt,fv,type)
- FV – Future value – formula: FV(rate,nper,pmt,pv,type)
- Rate – Interest rate per period – formula: RATE(nper,pmt,pv,fv,type)
- PMT – Payment made each period – formula: PMT(rate,nper,pv,fv,type)
- NPER – Total number of payment periods – formula: NPER(rate,pmt,pv,fv,type)
- Type – Begin mode =1 | End mode = 0
Note: End mode (0) for payments due at the end of the period while Begin mode (1) for payments due at the beginning of the period.
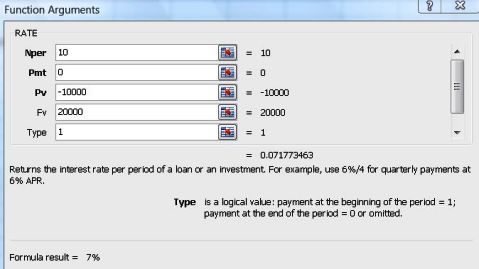
To clarify the misleading annual interest rate calculation above, I will show you a simple calculation using the Excel financial functions. In this case, we wanna looking for its real interest rate by performing RATE function.
From example above, Nper = 10 (period of 10 years), Pmt = 0 (no top-up in 10 years), Pv = -10000 ($10,000 cash taken out), Fv = 20000 ($20,000 received in the future), Type = 1 (Begin mode), so we use the formula as below:
formula: =RATE(10,0,-10000,20000,1)
Excel will show that the actual interest rate of the saving plan A is just 7 % rather than 10%. How much we can get if the plan A offers a true 10% interest rate? In this case, we’re looking for the future value by performing FV function. So the Rate = 10% or 0.1 (10% interest annually), Nper = 10 (10 years), Pmt = 0, Pv = -10000 ($10,000), Type = 1, and the formula will be:
Formula: =FV(10%,10,0,-10000,1)
We can get $25, 937.42 after 10 years at true annual compounding rate of 10%.
With functions above, you can easily perform quick calculation related to time and money such as compounding rates of fixed deposit, bond fund, saving endowment, saving accounts, dividend reinvest and more. In addition, you’re allowed to calculate the monthly installment for your housing loan, car loan and so forth via Microsoft Excel.
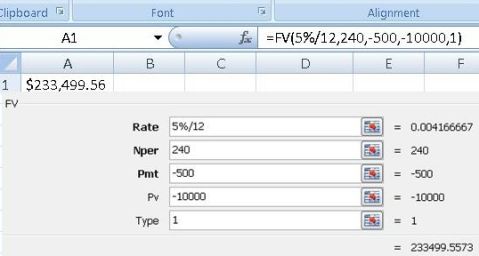
Example 1 (Future Value): If you invest $10,000 in a saving plan or unit trust fund which offers an estimated interest rate of 5%, and top up $500 every month for 20 years toward your retirement, how much you can get while retire? Formula to use: =FV(5%/12,240,-500,-10000,1) which returns $233,499.56.
- Rate = 5%/12 (5% annual interest rate divide by 12 months)
- Nper = 240 (20 years * 12 months = 240)
- Pmt = -500 (top up 500 monthly)
- Pv = -10000 ($10,000)
- Type = 1 (Begin mode)
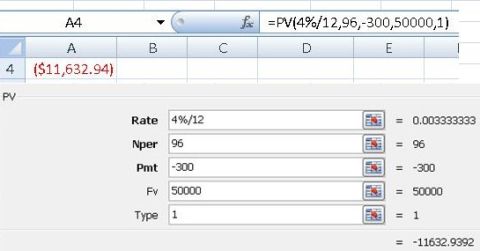
Example 2 (Present Value): For folks who wish to own $50,000 after 8 years, and willing to save $300 each month in an account with 4% interest rate, how much money they need to put into the account initially? Formula to use: =PV(4%/12,96,-300,50000,1) which returns $11,632.94.
- Rate = 4%/12
- Nper= 96 (month)
- Pmt = -300
- Fv = 50000
- Type= 1
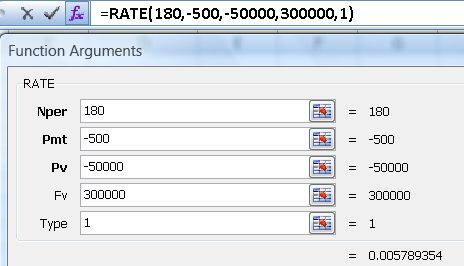
Example 3 (Interest Rate): If you wanna own $300,000 after 15 years, and willing to save $500 monthly with an initial investment amount of $50,000, What interest rate is needed to hit the goal? Formula to use: =RATE(180,-500,-50000,300000,1) which returns 5.8% interest rate.
- Nper = 180 (month)
- Pmt = -500 ($500)
- Pv = -50000 ($50,000)
- Fv = 300000 ($300,000)
- Type = 1
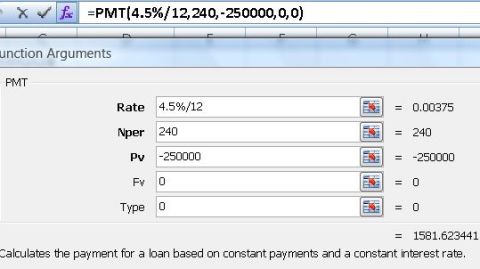
Example 4 (Payment): If you apply for personal loan, business loan, car loan or mortgage loan of $250,000 in 20-year period, based on 4.5% interest rate per year, how much you need to pay for the monthly installments? Formula to use: =PMT(4.5%/12,240,-250000,0,0) which returns $1,581.62.
- Rate = 4.5%/12
- Nper = 240 (month)
- Pv = -250000 ($250,000 loan)
- Fv = 0
- Type = 0
Note: Loans is normally under end mode.
Hopefully, the financial calculation tricks above can help you to choose a right and comprehensive investment or saving plan for living a great life.